This is part three of my series on fast searching and filtering of text using C#.
The previous article developed an indexing method using a hash table. This article develops a method using a trie structure. If you don’t know tries, I highly encourage to go read about them before continuing.
This filtering method is much more complex than previous versions, but we’ll take it one step at a time.
Trie Overview
Our data structure is more complex than a hash table, and definitely more involved than a simple list. We start with a data structure called a trie that contains a list of results, and links to the next nodes, indexed by letter. The key represented by a trie is determined by the path to that trie from the root. The root represents all keys and values (or none, depending on how you look at it). The trie is built up as we index items, beginning with an empty root. An illustration would be helpful about now:
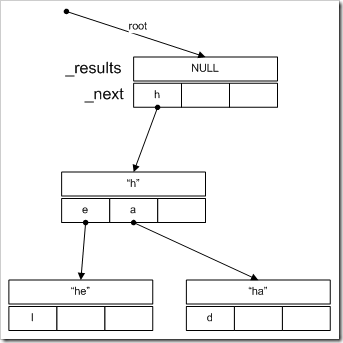
This diagram shows the top portion of an example trie structure. The root node has no results (since there are no values in the path to that node). The _next variable indexes the next links in the chain. Here, there is only one link–to ‘h’. The node with the value “h” has two further links–to ‘e’ and ‘a’.
So far, so good. However, in our implementation, we limit the depth of this tree to three so the results will potentially contain many entries. For example, if we followed the ‘l’ link in the “he” node, we would get to a node with the value “hel”. If we then indexed the word “hello”, the same node would then contain “hel” and “hello” because we’ve stopped the tree growth here. You can experiment with different values, but I found limited value beyond 3.
Adding Overview
To add a new item, we need to get substrings of the key, like usual, but unlike before, we don’t need to retrieve all substrings, just the longest substrings that aren’t the initial portions of a substring already found. Clear?
No? Here’s an example:
With the previous indexer (using the hash table), the substrings of “hello” would be:
h, he, hel, e, el, ell, l, ll, llo, lo, o
Now, think about our trie structure. Is there any reason to consider ‘h’ if we’re going to consider ‘he’ anyway? Why not just store our value under the results for “he”, and then if we filter on ‘h’ , just return the unified results of the ‘h’ node and every subnode under it. We’ve just cut our memory requirements substantially.
For a trie, we only need substrings of our tree height (or shorter if a longer one doesn’t exist–i.e., at the end of keys). If our maximum keylength/tree-height is 3, then the substrings required for “hello” are now just:
hel, ell, llo, lo, o
Nice.
Once we have these substrings, we can generate the trie, inserting our value (and full key) into the results of the bottom-most trie node we can reach, creating new trie nodes as necessary.
Looking up Overview
To find all values pertaining to a filter text, we start with the root node, and look up the filter text character by character, traversing the trie. If we run out of nodes, then there are no results. IF we run out of characters the results will include all the results in the current node as well as the results in subnodes.*
(*FYI: if we stored all the results in all applicable nodes, i.e., if we stored the value “Hello” in the nodes “hel”, “he” and “h”, we could speedup searches, BUT we’d use a lot more memory…and it would be exactly equivalent to the hash table implementation–we wouldn’t gain anything.)
Data Structures
With that overview out of the way, let’s cover the basic data structures we’ll need to pull this off.
The first is something we’re familiar with, the IndexStruct–which is actually a class like in the previous article:
1: private class IndexStruct
2: {
3: public UInt32 sortOrder;
4: public string key;
5: public T val;
6:
7: public IndexStruct(string key, T val, UInt32 sortOrder)
8: {
9: this.key = key;
10: this.val = val;
11: this.sortOrder = sortOrder;
12: }
13: };
This time, the sort order will be important as we’ll see below.
Trie
The next data structure we need is a trie. Technically, a trie is the whole tree, but since you can define a tree as a node with subtrees, it works to define a node too.
Here are the fields and properties we’ll need for the Trie class:
1: private class Trie
2: {
3: private char _val;
4: private Dictionary<char, Trie> _next = new Dictionary<char, Trie>();
5: private IList<IndexStruct> _results;
6:
7: #region Properties
8: public char Value
9: {
10: get
11: {
12: return _val;
13: }
14: set
15: {
16: _val = value;
17: }
18: }
19:
20: public IList<IndexStruct> Results
21: {
22: get
23: {
24: return _results;
25: }
26: }
27:
28: public Dictionary<char, Trie> Next
29: {
30: get
31: {
32: return _next;
33: }
34: }
35:
36: #endregion
37:
38: //...methods to follow...
39: }
The _val fields simply refers to the character this trie represents, though we don’t actually need it. I included it just for completeness. The _next dictionary associates the next character with another Trie object. The _results list stores all items that need to be stored in the current Trie object. The properties just wrap the fields.
The constructor is simple:
1: public Trie(char val)
2: {
3: _val = val;
4: }
We need a function to add a result to the trie’s list of results:
1: public void AddValue(IndexStruct indexStruct)
2: {
3: if (_results == null)
4: {
5: _results = new List<IndexStruct>();
6: }
7: _results.Add(indexStruct);
8: }
Notice, that the node only adds results to itself–it doesn’t try to figure out if a result belongs in itself or a sub-node in _next. To do that would require that each node have knowledge about keys as well as its place in the entire tree. This logic is better kept at a higher level.
We also need to associate a new trie node with a character:
1: public void AddNextTrie(char c, Trie nextTrie)
2: {
3: this.Next[c] = nextTrie;
4: }
OK, now we need to get into something more complex. We need a function to return all the results in the current trie, plus all the results in subnodes. Also, they should all be sorted. We could just return a huge list and sort them at the highest level with something like quicksort, but I have some additional knowledge about the data. I know that it’s being added in sorted order (since that’s how I define it. If it weren’t, we could presort each node anyway once indexing was done.) So let’s assume that each node’s results are already sorted. If that’s the case, we have an ideal setup for a merge sort!
Now, it’s entirely possible that just doing quicksort at the end would be faster, but in my tests at least, the merging seemed a little faster, especially since the results were mostly sorted, which is quicksort’s worst-case scenario.
So let’s define a helper function that takes two lists of IndexStruct and returns a single merged list:
1: private IList<IndexStruct> Merge(IList<IndexStruct> a, IList<IndexStruct> b)
2: {
3: if (a == null || a.Count == 0)
4: {
5: return b;
6: }
7: if (b == null || b.Count == 0)
8: {
9: return a;
10: }
11: int iA = 0, iB = 0;
12: List<IndexStruct> results = new List<IndexStruct>(a.Count + b.Count);
13: while (iA < a.Count || iB < b.Count)
14: {
15: if (iA < a.Count &&
16: (iB == b.Count || a[iA].sortOrder < b[iB].sortOrder))
17: {
18: results.Add(a[iA]);
19: iA++;
20: }
21: else if (iA<a.Count && iB<b.Count &&
22: a[iA].sortOrder == b[iB].sortOrder)
23: {
24: //if they're equal, make sure we skip the other
25: //one so we don't add it later
26: results.Add(a[iA]);
27: iA++;
28: iB++;
29: }
30: else
31: {
32: results.Add(b[iB]);
33: iB++;
34: }
35: }
36: return results;
37: }
This function interweaves the two arrays into a single array by always grabbing the smallest item from the next positions in the two lists. Look at lines 21-28. This is critical. We need to be on the lookout for identical sortorders, which indicate the same values. We don’t want to include those twice. This situation comes up when our value is “hi-ho” and we filter on “h”–results for both “hi” and “ho” will appear, and we don’t need both.
OK, so we we have a generic merge function. Now let’s make it work on the Trie:
1: public IList<IndexStruct> GetCombinedResults()
2: {
3: Queue<IList<IndexStruct>> queue = new Queue<IList<IndexStruct>>();
4: //first enqueue items in this node
5: if (_results != null && _results.Count > 0)
6: {
7: queue.Enqueue(_results);
8: }
9:
10: //get items from sub-nodes
11: foreach (Trie t in _next.Values)
12: {
13: IList<IndexStruct> r = t.GetCombinedResults();
14: queue.Enqueue(r);
15: }
16:
17: //merge all items together
18: while (queue.Count > 1)
19: {
20: IList<IndexStruct> a = queue.Dequeue();
21: IList<IndexStruct> b = queue.Dequeue();
22: queue.Enqueue(Merge(a, b));
23: }
24: return queue.Dequeue();
25: }
We maintain the list of items to merge together with a queue. We first enqueue the items in this node, then we call GetCombinedResults() for all subnodes, and enqueue those results. Finally, we merge the queued lists together, enqueueing the result, until a single list is formed.
Phew! OK, now let’s look at the rest of the indexer.
Some Helper Methods
RemoveUnneededCharacters is the same as before:
1: private string RemoveUnneededCharacters(string original)
2: {
3: char[] array = new char[original.Length];
4: int destIndex = 0;
5: for (int i = 0; i < original.Length; i++)
6: {
7: char c = original[i];
8: if (char.IsLetterOrDigit(c))
9: {
10: array[destIndex] = c;
11: destIndex++;
12: }
13: }
14: return new string(array, 0, destIndex);
15: }
We talked about our new version of GetSubStrings() above, and here it is:
1: private List<string> GetSubStrings(string key)
2: {
3: List<string> results = new List<string>();
4: //we only need to return substrings that
5: //themselves don't begin other substrings
6: //easy to do--return first _maxKeyLength characters
7: //or whatever's left, if shorter
8: for (int start = 0; start < key.Length; start++)
9: {
10: int len = Math.Min(_maxKeyLength, key.Length - start);
11: string sub = key.Substring(start, len);
12: //remove this if() to speed up index creation
13: //at the cost of slightly longer lookup time
14: if (key.IndexOf(sub) == start)
15: {
16: results.Add(sub);
17: }
18: }
19: return results;
20: }
As you can see, it’s mostly comments. Before we add our substring we make sure it’s the first occurence in the string of that particular sequence of characters (“don’t begin other substrings”). This prevents us from indexing “he” twice in the word “hehe”.
TrieIndexer
Now, to the real stuff! Actually, most of our work is done for us. So let’s declare our indexer:
1: class TrieIndexer<T> : IIndexer<T>
2: {
3: private Trie _rootTrie = new Trie(/*null char goes here--HTML doesn't like it/*);
4: private int _maxKeyLength = 3;
5:
6: public TrieIndexer(int maxKeyLength)
7: {
8: _maxKeyLength = maxKeyLength;
9: }
10: //..methods to follow...
11: }
We have our root trie node with a null character, and the constructor takes the maximum key length (which corresponds directly to the height of trie).
AddItem
1: public void AddItem(string key, T value, UInt32 sortOrder)
2: {
3: string toAdd = key.ToLower();
4:
5: toAdd = RemoveUnneededCharacters(toAdd);
6:
7: IndexStruct indexStruct = new IndexStruct(toAdd, value, sortOrder);
8:
9: List<string> subStrings = GetSubStrings(toAdd);
10:
11: foreach (string ss in subStrings)
12: {
13: Trie currentTrie = _rootTrie;
14: for (int i = 0; i < ss.Length; i++)
15: {
16: char c = ss[i];
17: Trie nextTrie = null;
18: if (!currentTrie.Next.TryGetValue(c, out nextTrie))
19: {
20: nextTrie = new Trie(c);
21: currentTrie.AddNextTrie(c, nextTrie);
22: }
23: currentTrie = nextTrie;
24: }
25: currentTrie.AddValue(indexStruct);
26: }
27: }
Lines 3-10 are the typical preprocessing of the key, and creating a structure for it and the value to live. The fun stuff happens in 12-30. With each substring, we begin at the root, and try to branch out node-by-node, character-by-character to find the bottom-most trie in which to place our indexed value. If the next one doesn’t exist, we create it. Once we get to the bottom of the tree for this subkey we add our value to the structure.
Lookup
Now let’s turn our attention to the filtering part. It’s almost like adding new values:
1: public IList<T> Lookup(string filterText)
2: {
3: Trie currentTrie = _rootTrie;
4:
5: int maxTrieLength = Math.Min(filterText.Length, _maxKeyLength);
6: for (int i = 0; i < maxTrieLength; i++)
7: {
8: Trie nextTrie = null;
9: if (currentTrie.Next.TryGetValue(filterText[i], out nextTrie))
10: {
11: currentTrie = nextTrie;
12: }
13: else
14: {
15: //no results
16: return new List<T>();
17: }
18: }
19: Debug.Assert(currentTrie != null);
20:
21: return GetResults(filterText, currentTrie);
22: }
We set our current node to the root. We then figure out the length of the path we need to traverse. If our filter text is longer than our maximum key length, we only want to go as far as the key length (and vice versa).
We do the same type of lookups as in AddItem, but this time if the next node isn’t present, we just return an empty list–there were no results for that filter text.
Once we find the target node, we call another function to actually compile the results for us:
1: private IList<T> GetResults(string filterText, Trie trie)
2: {
3: List<T> results = new List<T>();
4:
5: IList<IndexStruct> preResults = trie.GetCombinedResults();
6: if (preResults.Count <= 0)
7: {
8: return results;
9: }
10: results.Capacity = preResults.Count;
11: uint prevSortOrder = 0;
12: foreach (IndexStruct item in preResults)
13: {
14: Debug.Assert(item.sortOrder > prevSortOrder);
15: prevSortOrder = item.sortOrder;
16:
17: if (filterText.Length <= _maxKeyLength ||
18: item.key.IndexOf(filterText,
19: StringComparison.InvariantCultureIgnoreCase) >= 0)
20: {
21: results.Add(item.val);
22: }
23: }
24: return results;
25: }
In line 5, we call GetCombinedResults() and store it in the variable preResults. Why preResults? Why aren’t they final? For one, they are the entire IndexStruct object, and we still need to extract the values. Secondly, it’s possible the user entered a longer filter text than we indexed, so we still have to do a linear walk of the list and do string searches to make sure the preResult is really valid. Thankfully, we can avoid this if the filterText is short.
Summary
And now…we’re done! This one was a beast! There are still some optimizations to be found in here, but it’s pretty good. OK, so what about performance of this thing?
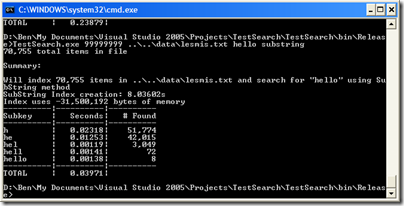
Let’s run it on lesmis.txt first:
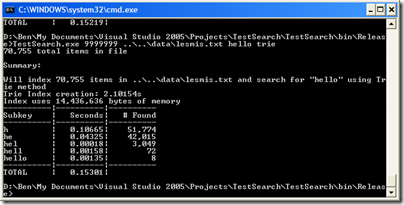
OK, for raw speed it’s actually slower than naive–overall. But look closer. Nearly ALL the time penalty is coming from the lookup of “h”. The next results are over ten times faster than naive. Now, let’s compare to the substring method. The trie method is overall slower still, and the search times are comparable (except for the initial search). But, look at memory usage: the trie method uses less than HALF what the substring method used. Also, the index creation time is 4 times faster. Mixed bag, but impressive none-the-less.
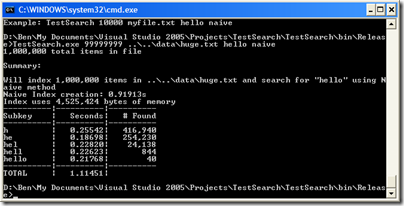
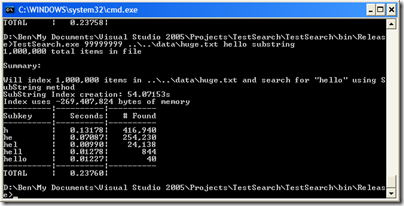
Now let’s run it on huge.txt:
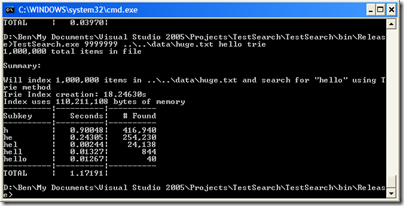
Ouch, over a second–but again, it’s all because of that initial search for “h”. All the other times are about the same. Comparing to the substring method, it uses almost a third of the memory, and takes a third of the time to create the index.
So what can we say about this method?
Pros:
- finding 0 results can be VERY fast (3-4 lookups in hash-tables to determine if a short filter text isn’t present).
- memory use is much better than enormous hash tables.
- Index creation time is better than other method.
- Searching for filter texts longer than a single character can be very fast.
Cons:
- short filter text is bad–has to combine lots of trie nodes.
(Note: in the course of writing this article, I changed my implementation to no longer need the Finish() function, which was part of the IIndexer<T> interface. I know I promised we’d use it, but I don’t need it!)
Download project files
Next time…
So where do we go from here? I have some notes about implementing this paired with a ListView control. Stay tuned for part 4!