Update: If you find this useful, you can read a much more complete treatment of garbage collection and performance in my book Writing High-Performance .NET Code.
Update: If you find this useful, you can read a much more complete treatment of garbage collection and performance in my book Writing High-Performance .NET Code.
Update: Part 2 – How to Debug GC Issues with PerfView is now available.
On this blog, I’ve alluded to the fact that I work on high-performance server applications, most recently in .Net. Writing these in .Net is just as possible as it is in native code, but it does come with its own set of challenges. In particular, one of the biggest things you need to learn how to deal with is garbage collection.
There is a lot out there already written about the CLR’s garbage collector, so I’m not going to go over many of the details. If you need a primer on it, MSDN has some documentation:
Read that first. For the rest of this article series, I will assume that you understand how the GC basically works.
In this and future articles, I’ll cover a lot of the stuff I’ve learned to improve application performance in the face of garbage collection.
Tip 1: Use Server GC
There are two modes of garbage collection (GC): workstation and server. As long as you’re running multiple processors, you almost certainly want server mode collection. With workstation mode, a GC happens on the thread that makes the allocation that causes the GC. The collection happens at normal priority.
With server GC, a thread for every core is created just for doing GC. There is also a small object heap and a large object heap created for each GC thread. All of the program’s allocations are spread among these heaps (more on large object heaps later). When no GC is happening, these threads are blocked and do nothing. When a GC is triggered, all of the user threads get paused, and all the GC threads wake up at highest priority and do collection in parallel. All of these optimizations lead to server GC usually being much faster than workstation GC.
A word about concurrent collections: In workstation GC, concurrent collections are enabled by default. However, this only applies to generation 2 collections. Generations 0 and 1 are always blocking. However, given that it’s concurrent, that means that it will compete with your own threads that are trying to get actual work done. In a high-performance server scenario, that may not be acceptable. A better strategy is to ensure that generation 2 collections never (or extremely rarely) happen.
You enable server GC by putting this in app.config:
<configuration> <runtime> <gcServer enabled="true"/> </runtime> </configuration>
Tip 2: Objects Live Briefly or Forever
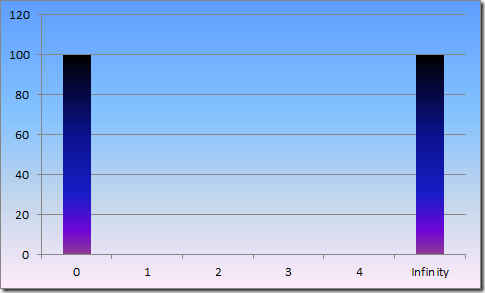
A histogram of object lifetimes in your app should look essentially like this:
Object last either a vanishingly brief amount of time, or they last forever – it’s the stuff in the middle that will kill your performance.
This has everything to do with the generations of garbage collection and object survivorship. There are three generations: 0, 1, and 2. Generation 0 happens most often and is the fastest—ideally lasting only a couple of milliseconds, if that. Objects that didn’t get cleaned up in generation 0 are put into generation 1. Generation 1 collections are also very fast, usually as fast as generation 0. The problem, though, is that objects that make it to generation 1 have a fair chance of surviving this generation, and being put into generation 2.
Generation 2 is the problem. A generation 2 collection is much slower than 0 or 1—often on the order of hundreds of milliseconds or even seconds—that means your process is paused completely for that time. You do not want objects to survive to generation 2.
So how often do collections happen? There is no hard-and-fast rule: it all depends on your allocation rate, memory pressure, and patterns that you’ve trained into the GC. The GC will adapt over time, training itself on your memory usage patterns. All of this completely depends on your application and I’ll look at ways to measure all of this in a future article.
Tip 3: All Long-Lived Objects Must Be Pooled
It may be that you can’t ensure all objects for a given request are cleaned up in the first generation 0 collection that occurs. If requests are in memory longer than the time between collections, then you’re guaranteed to have survivorship.
For these types of objects, first see if you can factor them so that not all parts them have to live that long. Control object lifetime very closely and null out references once you’re done.
Once you’ve done that, hopefully there are only a handful of objects that really must last the entire length of a request. For those, create a pool of them with reinitialization semantics—effectively move them to the far end of that histogram above, where they live forever.
This works because of the adaptive nature of the garbage collector – it learns over time that if it does a collection and doesn’t free up much memory, it will schedule that generation of collection to happen less frequently. In my own case, at one point, our server had trained the GC to do a generation 2 collection less often than once per day, under a constant load. With enough work, we could probably get that to essentially never.
You may be able to get quite far without the need to implement object pooling. Or you may need to pool only a small number of objects, and the survivorship of the remaining objects is not enough to cause problematic garbage collections—only measurement and observation will tell you for sure.
Tip 4: All Large Objects Must Be Pooled
There is a way to cause an object to automatically be in generation 2: make it at least 85000 bytes in size. Anything at least that size gets put into a Large Object Heap. Only generation 2 collections service that type of heap.
Want to cause a generation 2 collection? Do this:
byte[] buffer = new byte[85000];
If you want high-performance, you absolutely cannot do this per request on a server. These types of buffers, or other large objects, must be pooled. There is no built-in pooling mechanism in .Net—you must write your own. There are usually not too many large objects you’ll need to pool: strings and byte buffers are the usual suspects, if you need to do much serialization/deserialization, but also look out for collections of any type.
If you want to know more about the Large Object Heap and why 85000 bytes is the threshold, read this great article: Large Object Heap Uncovered.
Pooling collection objects comes with its own set of challenges:
- You can’t assume the full collection is valid (the difference between length and capacity). If you use pooled arrays, for example, you have to track the length separately, since only a small portion of the array may be valid. This can drastically affect the interfaces between components.
- Pooled collections that can grow over time will cause your memory to rise indefinitely unless you put limits on the size of the pool and/or the size of collections within the pool.
- Large Object Heaps are not compacted during collection, which means that you can fragment the heap such that it’s wasting a lot of memory. It all depends on your allocation and collection pattern. I may talk about heap fragmentation in another article.
Once you solve those, you’re good to go… no more generation 2 collections!
Next Time…
In my next article, I’ll cover tools you can use to measure garbage collection statistics, and how you can use that knowledge to improve your performance.